6. อาเรย์ 1-3 มิติ (ยกเว้น cell array)
ในหัวข้อนี้เราจะเรียนเฉพาะอาเรย์ของตัวเลข และอาเรย์ของตัวอักษรเท่านั้น ส่วน cell อาเรย์นั้นจะเรียนในหลักสูตรพื้นฐาน 2 ส่วนหลักสูตรปัจจุบันที่ผู้อ่านกำลังศึกษาอยู่นี้คือ หลักสูตรพื้นฐาน 1
เมื่ออาเรย์สามารถเก็บค่าได้หลายค่า ดังนั้นโครงสร้างของมันจึงซับซ้อนกว่าตัวแปรทั่วไป ซึ่งความซับซ้อนของอาเรย์นั้นจะถูกแบ่งออกตามมิติ ของอาเรย์นั้นๆ โดยอาเรย์ 1-3 มิติ มีโครงสร้างดังนี้
รูปนี้หมายความว่า ตัวแปรอารย์นี้ชื่อว่า A มีสมาชิกทั้งหมด 4 ตัว ตัวที่ 1 คือ 5 และตัวที่ 4 คือ 17 เมื่อเราต้องการดึงค่า หรือกำหนดค่า เข้าไปในอาเรย์ เราจะเรียกกระบวนการนี้ว่า “การเข้าถึงข้อมูลในอาเรย์” ซึ่งสามารถทำได้ง่ายๆ โดยการพิมพ์ชื่อตัวแปรอาเรย์ต่อท้ายด้วยวงเล็บ และตำแหน่งของข้อมูลที่ต้องการเข้าถึง เช่น
>> disp(A(2))
หมายความว่าให้แสดงค่าของอาเรย์ A ตำแหน่งที่ 2 ซึ่งผลลัพธ์ที่ได้คือ 2.5
>> A(3) = A(3)+1
หมายความว่าให้ตำแหน่งที่ 3 ในอาเรย์ A เก็บค่า 9+1 ซึ่งมีค่าเท่ากับ 10
>> A(3) = A(3+1)
หมายความว่าให้ตำแหน่งที่ 3 ในอาเรย์ A เก็บค่า 17
ในรูปนี้หมายความว่า อาเรย์ 2 มิตินี้มีชื่อว่า A และการเข้าถึงข้อมูลในอาเรย์ ทำได้เช่นเดียวกับอาเรย์ 1 มิติ นั่นก็คือ วงเล็บ และตามด้วยตำแหน่ง แต่เนื้องจากอาเรย์ 2 มิติ มีทั้งแถว และคอลัมภ์ ดังนั้นเวลาเข้าถึงข้อมูล จึงจำเป็นต้องระบุตำแหน่งแถว และคอลัมภ์ด้วย ซึ่งโดยปกติแล้วจะใช้ตัว m แทนแถว และ n แทนคอลัมภ์ เช่น
>> disp(A(2,1))
ผลลัพธ์ที่ได้ก็คือ 1
>> A(2,1) = A(1,1)+2
หมายความว่าให้เก็บค่า 2+2 ซึ่งมีค่าเท่ากับ 4 ไปไว้ในตำแหน่งแถวที่ 2 คอลัมภ์ที่ 1 ในอาเรย์ A
>> A(2,1+2) = A(1,1+2)
หมายความว่า ให้เก็บค่า 4 ไว้ในอาเรย์ A แถวที่ 2 คอลัมภ์ที่ 3
อาเรย์ประเภทนี้ มีลักษณะโครงสร้างเหมือนเอาอาเรย์ 2 มิติมาวางซ้อนกัน ทำให้อาเรย์มีหลายชั้น ซึ่งแต่ละชั้นเรียกว่า “เลเยอร์” โดยปกติแล้วจะพบได้ในข้อมูลของรูปภาพ แต่หากเป็นการเขียนโปรแกรมตามปกติ ผมแนะนำว่าให้หลีกเลี่ยงการใช้งานประเภทนี้ถ้าทำได้ เพราะในการเขียนโปรแกรมจริงๆ นั้น เราต้องจำเอาไว้ด้วยว่า แต่ละตำแหน่งของอาเรย์ เราเก็บข้อมูลอะไรเอาไว้ เช่น ถ้าเรากำหนดให้อาเรย์ A เป็นตัวแปรที่เอาไว้เก็บค่าบริการของลูกหาบ ที่ให้บริการหาบของขึ้นภูกระดึง โดยคอลัมภ์ที่ 1, 2, 3 แทนระยะทาง 1, 2, 3 กิโลเมตร ส่วนแถวที่ 1, 2, 3 แทนน้ำหนักของ 1, 2, 3 กิโลกรัม และเลเยอร์ แทนจำนวนชิ้น โดยเลเยอร์ที่ 1, 2, 3 แทนจำนวนสิ่งของ 1, 2, 3 ชิ้น ตามลำดับ ดังนั้น หากเราต้องการจ้างลูกหาบ หาบสิ่งของที่มีน้ำหนัก 2 กิโลกรัม จำนวน 2 ชิ้น เป็นระยะทาง 3 กิโลเมตร เราก็ต้องดูราคาค่าบริการที่ A(2,3,2) เท่านั้น
ดังนั้นจะเห็นว่า หากเราเลือกใช้อาเรย์ที่มีโครงสร้างซับซ้อน เราซึ่งเป็นผู้เขียนก็ต้องจำโครงสร้างและความหมายของแต่ละตำแหน่งให้ได้ด้วย ดังนั้นผมจึงแนะนำว่า ถ้าไม่จำเป็นจริงๆ ก็ใช้แค่อาเรย์ 2 มิติก็พอแล้ว และไม่ต้องไปคิดถึงอาเรย์ 4 มิติ 5 มิติ หรือมากกว่านั้น ถึงแม้ในทางทฤษฎีเราจะสามารถสร้างอาเรย์พวกนี้ขึ้นมาใช้งานได้จริง แต่ในทางปฎิบัตินั้นมันจะทำให้เราสับสนมาก
ดังนั้นหากเราจำเป็นต้องใช้อาเรย์ 4 มิติจริงๆ ให้เปลี่ยนไปใช้ cell อาเรย์จะดีกว่า ตัวอย่างเช่น ถ้าเราต้องการเก็บรูปภาพหลายๆ รูปเอาไว้ในตัวแปรเดียวกัน แน่นอนว่าตัวแปรนั้นจะต้องเป็นอาเรย์ และเนื่องจากข้อมูลของรูปภาพนั้น ปกติจะเป็นอาเรย์ 3 มิติอยู่แล้ว เราก็ต้องใช้มิติที่ 4 เพื่อแบ่งรูปภาพที่ 1 ถึง n ซึ่งจริงๆ แล้วเราก็สามารถทำได้ แต่ผมแนะนำว่าเอาแต่ละรูปไปเก็บไว้ใน cell อาเรย์จะง่ายกว่า เพราะอาเรย์ปกตินั้น มีเงื่อนไขที่สำคัญ ดังต่อไปนี้
2. จำนวนคอลัมภ์ของทุกแถวต้องเท่ากันเสมอ
3. จำนวนแถว ของทุกคอลัมภ์ ต้องเท่ากันเสมอ
4. จำนวนแถว และคอลัมภ์ของทุกเลเยอร์ ต้องเท่ากันเสมอ
ดังนั้นหากเราจะใช้อาเรย์ 4 มิติเก็บรูปภาพ รูปภาพเหล่านั้นต้องมีขนาดเท่ากัน จึงจะสามารถเก็บเอาไว้ด้วยกันได้ แต่หากเราใช้ cell อาเรย์ เงื่อนไขต่างๆ เหล่านี้จะหายไปทั้งหมด
ตัวอย่างนี้คือการสร้างอาเรย์ 1 มิติ ซึ่งหากเราไม่ต้องการเขียน comma (,) เราสามารถเขียนโดยเว้นช่องว่างเอาไว้ก็ได้ ซึ่งจะให้ความหมายเหมือนกันกับการใช้ comma
>> A = [1 2;3 4];
ตัวอย่างนี้คือการสร้างอาเรย์ 2 มิติ ซึ่งเราแบ่งแต่ละบรรทัดโดยใช้ semi-colon (;)
>> A(:, :, 1) = [1 2;3 4];
>> A(:, :, 2) = [5 6;7 8];
ตัวอย่างนี้คือการสร้างอาเรย์ 3 มิติ ซึ่งเราต้องสร้างขึ้นมาทีละเลเยอร์
แต่การสร้างอาเรย์แบบป้อนข้อมูลเองทั้งหมด มันก็ค่อนข้างเสียเวลาหากเราต้องสร้างอาเรย์ขนาดใหญ่ ดังนั้นจึงเป็นที่มาของวิธีที่ 2
>> A = 1:40;
หมายความว่า A เป็นอาเรย์ 1 มิติ มีค่าเป็น 1,2,3,4,…,40 (เพิ่มทีละ 1)
>> B = 1:2:40;
หมายความว่า B เป็นอาเรย์ 1 มิติ มีค่าเป็น 1,3,5,7,…,39 (เพิ่มทีละ 2)
ส่วนการสร้างอาเรย์ 2 มิติ และ 3 มิตินั้น เราจะใช้การรวมอาเรย์ ซึ่งจะกล่าวในหัวข้อถัดไป
- rand(m,n)
- randi([x,y],m,n)
- zeros(m,n)
- k*ones(m,n)
จริงๆ แล้วคำสั่ง ones ใช้สร้างแมททริกซ์ที่มีแต่เลข 1 ซึ่งถ้าเราอยากได้แมททริกซ์ค่าอื่นๆ เราก็แค่เอา k ซึ่งเป็นค่าคงที่ใดๆ เข้าไปคูณเท่านั้นเอง
1. การรวมแบบต่อด้านข้าง การรวมแบบนี้มีเงื่อนไขว่าอาเรย์ที่นำมารวมกัน จะต้องมีจำนวนแถวเท่ากัน
2. การรวมแบบต่อด้านล่าง การรวมแบบนี้มีเงื่อนไขว่า อาเรย์ที่นำมารวมกัน จะต้องมีจำนวนคอลัมภ์เท่ากัน
ตัวอย่างเช่น
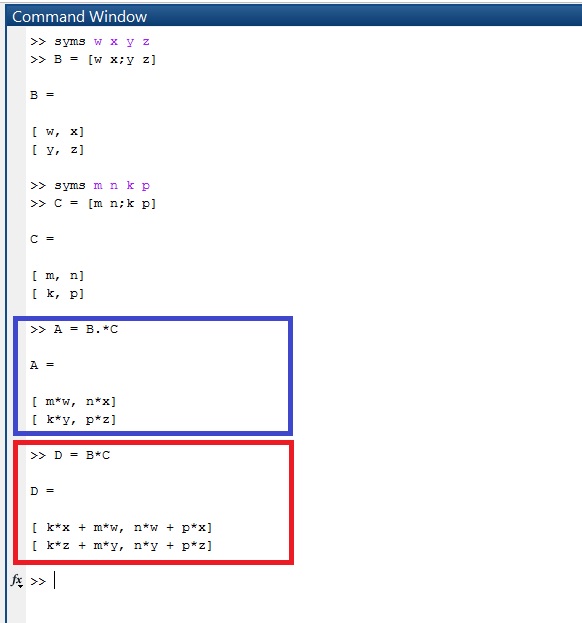
ในตัวอย่างนี้ A คือการสร้างอาเรย์ 1 มิติ แบบใช้ตัวช่วยสร้าง ส่วน B คือการสร้างอาเรย์ 2 มิติที่ใช้คำสั่ง ส่วน C คือการรวมอาเรย์แบบที่ 2 โดยเอา A มาต่อด้านล่าง A ส่วน D คือการรวม C กับ B โดยเอา B มาต่อด้านซ้ายของ C
การรวมอาเรย์นั้นจะเห็นว่าต้องเป็นไปตามเงื่อนไข 2 ข้อนั้นเสมอ ถึงจะสามารถรวมกันได้ และใช้เครื่องหมาย [ ] ในการรวมอาเรย์เข้าด้วยกัน ส่วนวิธีการรวมกันนั้นเหมือนกับการสร้างอาเรย์แบบป้อนข้อมูลเอง คือ หากรวมแบบต่อด้านข้าง จะใช้ comma หรือ ช่องว่าง เพื่อแบ่งแยกตัวแปร ส่วนการรวมกันแบบต่อด้านล่าง หรือ ด้านบน จะใช้ semi-colon เพื่อแบ่งแยกตัวแปร
6.1 อาเรย์ คือ อะไร
อาเรย์ คือ ชุดของข้อมูลประเภทเดียวกัน ซึ่งหมายความว่ามันสามารถเก็บค่าเอาไว้ได้หลายค่าในตัวแปรตัวเดียว แตกต่างจากตัวแปรทั่วไปที่เราเรียนมาก่อนหน้านี้ เพราะถ้าสังเกตุให้ดี เราจะเห็นว่าตัวแปรทั่วไปนั้น สามารถเก็บค่าได้ 1 ค่าเท่านั้นเมื่ออาเรย์สามารถเก็บค่าได้หลายค่า ดังนั้นโครงสร้างของมันจึงซับซ้อนกว่าตัวแปรทั่วไป ซึ่งความซับซ้อนของอาเรย์นั้นจะถูกแบ่งออกตามมิติ ของอาเรย์นั้นๆ โดยอาเรย์ 1-3 มิติ มีโครงสร้างดังนี้
อาเรย์ 1 มิติ หรือเรียกอีกชื่อว่า Vector
รูปนี้หมายความว่า ตัวแปรอารย์นี้ชื่อว่า A มีสมาชิกทั้งหมด 4 ตัว ตัวที่ 1 คือ 5 และตัวที่ 4 คือ 17 เมื่อเราต้องการดึงค่า หรือกำหนดค่า เข้าไปในอาเรย์ เราจะเรียกกระบวนการนี้ว่า “การเข้าถึงข้อมูลในอาเรย์” ซึ่งสามารถทำได้ง่ายๆ โดยการพิมพ์ชื่อตัวแปรอาเรย์ต่อท้ายด้วยวงเล็บ และตำแหน่งของข้อมูลที่ต้องการเข้าถึง เช่น
>> disp(A(2))
หมายความว่าให้แสดงค่าของอาเรย์ A ตำแหน่งที่ 2 ซึ่งผลลัพธ์ที่ได้คือ 2.5
>> A(3) = A(3)+1
หมายความว่าให้ตำแหน่งที่ 3 ในอาเรย์ A เก็บค่า 9+1 ซึ่งมีค่าเท่ากับ 10
>> A(3) = A(3+1)
หมายความว่าให้ตำแหน่งที่ 3 ในอาเรย์ A เก็บค่า 17
อาเรย์ 2 มิติ หรือ เรียกอีกชื่อว่า Matrix
ในรูปนี้หมายความว่า อาเรย์ 2 มิตินี้มีชื่อว่า A และการเข้าถึงข้อมูลในอาเรย์ ทำได้เช่นเดียวกับอาเรย์ 1 มิติ นั่นก็คือ วงเล็บ และตามด้วยตำแหน่ง แต่เนื้องจากอาเรย์ 2 มิติ มีทั้งแถว และคอลัมภ์ ดังนั้นเวลาเข้าถึงข้อมูล จึงจำเป็นต้องระบุตำแหน่งแถว และคอลัมภ์ด้วย ซึ่งโดยปกติแล้วจะใช้ตัว m แทนแถว และ n แทนคอลัมภ์ เช่น
>> disp(A(2,1))
ผลลัพธ์ที่ได้ก็คือ 1
>> A(2,1) = A(1,1)+2
หมายความว่าให้เก็บค่า 2+2 ซึ่งมีค่าเท่ากับ 4 ไปไว้ในตำแหน่งแถวที่ 2 คอลัมภ์ที่ 1 ในอาเรย์ A
>> A(2,1+2) = A(1,1+2)
หมายความว่า ให้เก็บค่า 4 ไว้ในอาเรย์ A แถวที่ 2 คอลัมภ์ที่ 3
อาเรย์ 3 มิติ
อาเรย์ประเภทนี้ มีลักษณะโครงสร้างเหมือนเอาอาเรย์ 2 มิติมาวางซ้อนกัน ทำให้อาเรย์มีหลายชั้น ซึ่งแต่ละชั้นเรียกว่า “เลเยอร์” โดยปกติแล้วจะพบได้ในข้อมูลของรูปภาพ แต่หากเป็นการเขียนโปรแกรมตามปกติ ผมแนะนำว่าให้หลีกเลี่ยงการใช้งานประเภทนี้ถ้าทำได้ เพราะในการเขียนโปรแกรมจริงๆ นั้น เราต้องจำเอาไว้ด้วยว่า แต่ละตำแหน่งของอาเรย์ เราเก็บข้อมูลอะไรเอาไว้ เช่น ถ้าเรากำหนดให้อาเรย์ A เป็นตัวแปรที่เอาไว้เก็บค่าบริการของลูกหาบ ที่ให้บริการหาบของขึ้นภูกระดึง โดยคอลัมภ์ที่ 1, 2, 3 แทนระยะทาง 1, 2, 3 กิโลเมตร ส่วนแถวที่ 1, 2, 3 แทนน้ำหนักของ 1, 2, 3 กิโลกรัม และเลเยอร์ แทนจำนวนชิ้น โดยเลเยอร์ที่ 1, 2, 3 แทนจำนวนสิ่งของ 1, 2, 3 ชิ้น ตามลำดับ ดังนั้น หากเราต้องการจ้างลูกหาบ หาบสิ่งของที่มีน้ำหนัก 2 กิโลกรัม จำนวน 2 ชิ้น เป็นระยะทาง 3 กิโลเมตร เราก็ต้องดูราคาค่าบริการที่ A(2,3,2) เท่านั้น
ดังนั้นจะเห็นว่า หากเราเลือกใช้อาเรย์ที่มีโครงสร้างซับซ้อน เราซึ่งเป็นผู้เขียนก็ต้องจำโครงสร้างและความหมายของแต่ละตำแหน่งให้ได้ด้วย ดังนั้นผมจึงแนะนำว่า ถ้าไม่จำเป็นจริงๆ ก็ใช้แค่อาเรย์ 2 มิติก็พอแล้ว และไม่ต้องไปคิดถึงอาเรย์ 4 มิติ 5 มิติ หรือมากกว่านั้น ถึงแม้ในทางทฤษฎีเราจะสามารถสร้างอาเรย์พวกนี้ขึ้นมาใช้งานได้จริง แต่ในทางปฎิบัตินั้นมันจะทำให้เราสับสนมาก
ดังนั้นหากเราจำเป็นต้องใช้อาเรย์ 4 มิติจริงๆ ให้เปลี่ยนไปใช้ cell อาเรย์จะดีกว่า ตัวอย่างเช่น ถ้าเราต้องการเก็บรูปภาพหลายๆ รูปเอาไว้ในตัวแปรเดียวกัน แน่นอนว่าตัวแปรนั้นจะต้องเป็นอาเรย์ และเนื่องจากข้อมูลของรูปภาพนั้น ปกติจะเป็นอาเรย์ 3 มิติอยู่แล้ว เราก็ต้องใช้มิติที่ 4 เพื่อแบ่งรูปภาพที่ 1 ถึง n ซึ่งจริงๆ แล้วเราก็สามารถทำได้ แต่ผมแนะนำว่าเอาแต่ละรูปไปเก็บไว้ใน cell อาเรย์จะง่ายกว่า เพราะอาเรย์ปกตินั้น มีเงื่อนไขที่สำคัญ ดังต่อไปนี้
เงื่อนไขสำคัญของอาเรย์ทุกประเภท
1. ข้อมูลในอาเรย์จะต้องเป็นประเภทเดียวกัน เช่น ถ้าเป็นตัวเลข ก็ต้องเป็นตัวเลขทั้งหมด ถ้าเป็นตัวอักษร ก็ต้องเป็นตัวอักษรทั้งหมด2. จำนวนคอลัมภ์ของทุกแถวต้องเท่ากันเสมอ
3. จำนวนแถว ของทุกคอลัมภ์ ต้องเท่ากันเสมอ
4. จำนวนแถว และคอลัมภ์ของทุกเลเยอร์ ต้องเท่ากันเสมอ
ดังนั้นหากเราจะใช้อาเรย์ 4 มิติเก็บรูปภาพ รูปภาพเหล่านั้นต้องมีขนาดเท่ากัน จึงจะสามารถเก็บเอาไว้ด้วยกันได้ แต่หากเราใช้ cell อาเรย์ เงื่อนไขต่างๆ เหล่านี้จะหายไปทั้งหมด
6.2 การสร้างอาเรย์
ผมแบ่งการสร้างอาเรย์ออกเป็น 3 วิธีด้วยกัน คือ1. สร้างอาเรย์ โดยการป้อนข้อมูลเองทั้งหมด
>> A = [1, 2, 3, 4];ตัวอย่างนี้คือการสร้างอาเรย์ 1 มิติ ซึ่งหากเราไม่ต้องการเขียน comma (,) เราสามารถเขียนโดยเว้นช่องว่างเอาไว้ก็ได้ ซึ่งจะให้ความหมายเหมือนกันกับการใช้ comma
>> A = [1 2;3 4];
ตัวอย่างนี้คือการสร้างอาเรย์ 2 มิติ ซึ่งเราแบ่งแต่ละบรรทัดโดยใช้ semi-colon (;)
>> A(:, :, 1) = [1 2;3 4];
>> A(:, :, 2) = [5 6;7 8];
ตัวอย่างนี้คือการสร้างอาเรย์ 3 มิติ ซึ่งเราต้องสร้างขึ้นมาทีละเลเยอร์
แต่การสร้างอาเรย์แบบป้อนข้อมูลเองทั้งหมด มันก็ค่อนข้างเสียเวลาหากเราต้องสร้างอาเรย์ขนาดใหญ่ ดังนั้นจึงเป็นที่มาของวิธีที่ 2
2. สร้างอาเรย์ โดยใช้ตัวช่วย
เราสามารถใช้เครื่องหมาย colon ( : ) เพื่อช่วงสร้างอาเรย์ได้ เช่น>> A = 1:40;
หมายความว่า A เป็นอาเรย์ 1 มิติ มีค่าเป็น 1,2,3,4,…,40 (เพิ่มทีละ 1)
>> B = 1:2:40;
หมายความว่า B เป็นอาเรย์ 1 มิติ มีค่าเป็น 1,3,5,7,…,39 (เพิ่มทีละ 2)
ส่วนการสร้างอาเรย์ 2 มิติ และ 3 มิตินั้น เราจะใช้การรวมอาเรย์ ซึ่งจะกล่าวในหัวข้อถัดไป
3. สร้างอาเรย์ โดยใช้คำสั่ง
คำสั่งสร้างอาเรย์นั้นมีอยู่หลายคำสั่ง แต่ที่ผมได้ใช้บ่อยๆ มีดังนี้- rand(m,n)
- randi([x,y],m,n)
- zeros(m,n)
- k*ones(m,n)
จริงๆ แล้วคำสั่ง ones ใช้สร้างแมททริกซ์ที่มีแต่เลข 1 ซึ่งถ้าเราอยากได้แมททริกซ์ค่าอื่นๆ เราก็แค่เอา k ซึ่งเป็นค่าคงที่ใดๆ เข้าไปคูณเท่านั้นเอง
6.3 การรวมอาเรย์
การรวมอาเรย์นั้นมี 2 แบบคือ1. การรวมแบบต่อด้านข้าง การรวมแบบนี้มีเงื่อนไขว่าอาเรย์ที่นำมารวมกัน จะต้องมีจำนวนแถวเท่ากัน
2. การรวมแบบต่อด้านล่าง การรวมแบบนี้มีเงื่อนไขว่า อาเรย์ที่นำมารวมกัน จะต้องมีจำนวนคอลัมภ์เท่ากัน
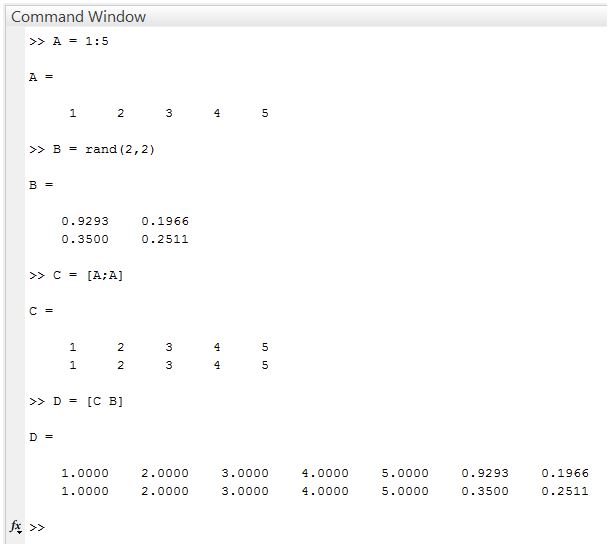
ตัวอย่างเช่น
ในตัวอย่างนี้ A คือการสร้างอาเรย์ 1 มิติ แบบใช้ตัวช่วยสร้าง ส่วน B คือการสร้างอาเรย์ 2 มิติที่ใช้คำสั่ง ส่วน C คือการรวมอาเรย์แบบที่ 2 โดยเอา A มาต่อด้านล่าง A ส่วน D คือการรวม C กับ B โดยเอา B มาต่อด้านซ้ายของ C
การรวมอาเรย์นั้นจะเห็นว่าต้องเป็นไปตามเงื่อนไข 2 ข้อนั้นเสมอ ถึงจะสามารถรวมกันได้ และใช้เครื่องหมาย [ ] ในการรวมอาเรย์เข้าด้วยกัน ส่วนวิธีการรวมกันนั้นเหมือนกับการสร้างอาเรย์แบบป้อนข้อมูลเอง คือ หากรวมแบบต่อด้านข้าง จะใช้ comma หรือ ช่องว่าง เพื่อแบ่งแยกตัวแปร ส่วนการรวมกันแบบต่อด้านล่าง หรือ ด้านบน จะใช้ semi-colon เพื่อแบ่งแยกตัวแปร
จบหัวข้อที่ 6